JChiffresFX – A Chiffres Game solver

JChiffresFX is an application for solving the »Chiffres« part of the game »Des chiffres et des lettres«. It will find all solutions (in the form of a sequence of binary operations) while filtering out duplicate and redundant solutions.

Here you can see some screenshots:

1 2 3 4 5 6 7

New in version 3.0

  • It is possible to save the selected solution graphic in the file formats PNG, JPG, BMP, TIFF and SVG with miscellaneous options.
  • It is possible to save the solution table to a CSV file.
  • Miscellaneous detail improvements (user interface, performance fine tuning, internal maintenance …).

New in version 2.1

  • Miscellaneous user interface related detail improvements.

New in version 2.0

  • An extended calculation parameter input to use operands and calculation targets of a broader range and up to 9 operands.
  • A parallelized algorithm to take advantage of all available CPU cores.
  • Minor miscellaneous user interface improvements.
Documentation

The objective of the game is to calculate (in your head and with a time limit, e.g. 40 seconds) a given three digit number from 6 given numbers (in the range 1 to 10, 25, 50, 75, 100) using elementary arithmetic. Each of the given 6 operands must be used at most once.

Example

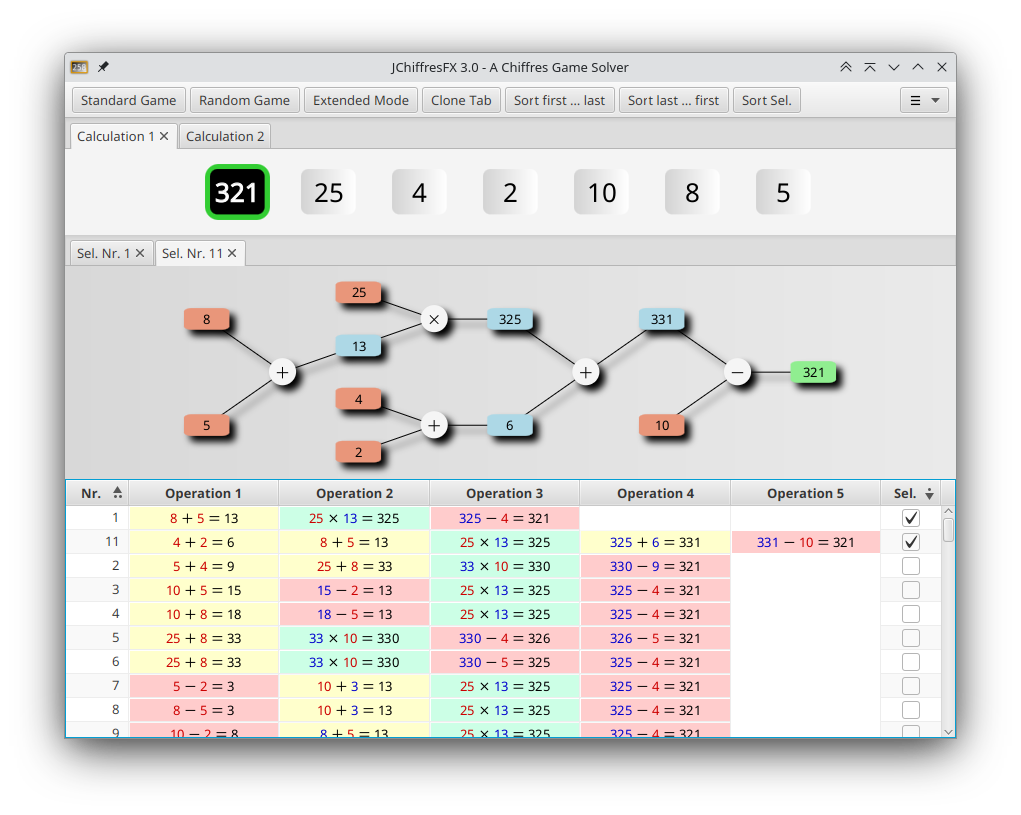
Let the numbers given be 25, 4, 2, 10, 8, 5 with the calculation goal 321. Then there is a possible solution:

  8 +  5 =  13
 25 * 13 = 325
325 -  4 = 321
Calculation example

The user interface has 3 modes with the following characteristics:

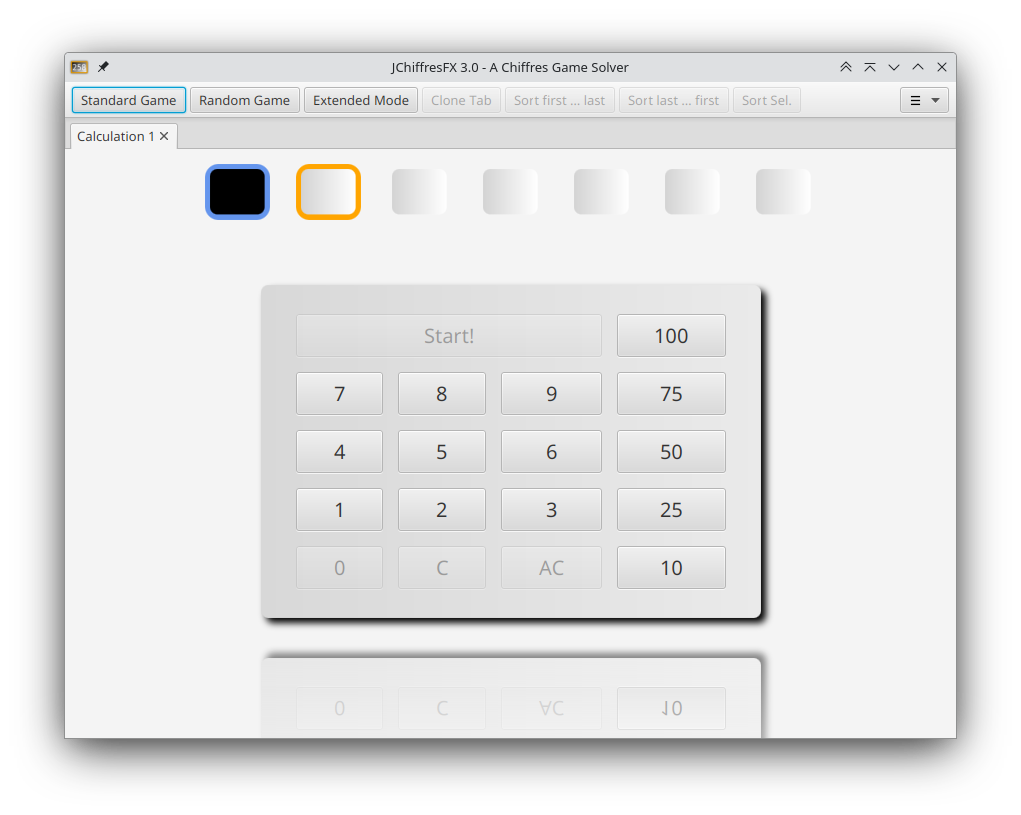
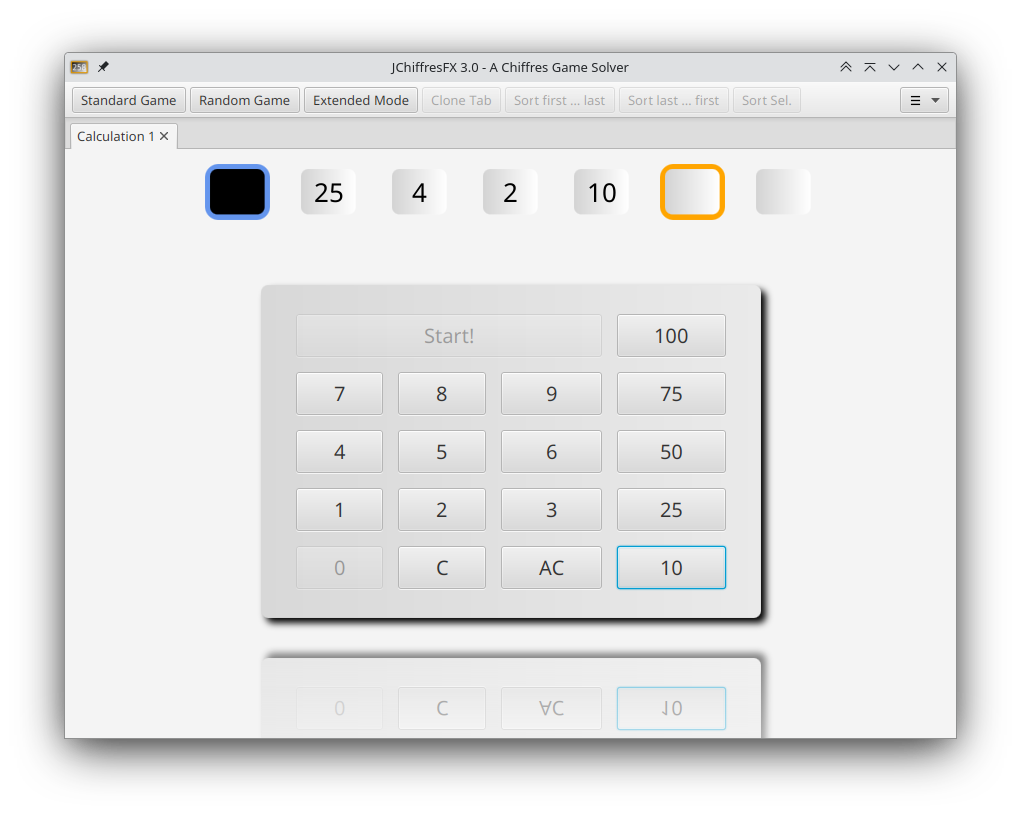
Standard Game

The Toolbar-Button »Standard Game« opens a new tab to input a game according to the standard rules with simple mouse clicks. After a click on »Start!« all possible solutions will be calculated and displayed in a table, filtering out duplicate and redundant solutions. The solution in the selected table row will be displayed graphically. It is also possible to mark solutions with a checkbox. Those selected solutions will be accessible through tabs in the graphical view, and a click on »Sort Sel.« will sort them to the beginning of the table.

Random Game

The Toolbar-Button »Random Game« opens a new tab with given random numbers which otherwise works like the tab »Standard Game«.

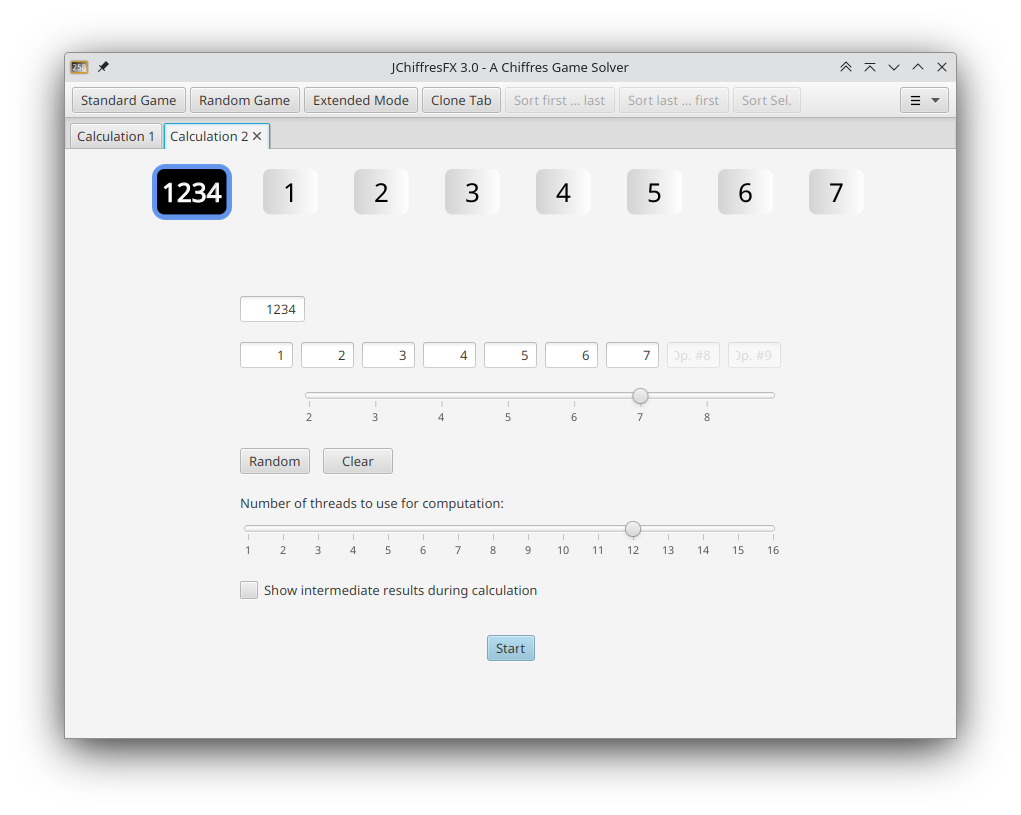
Extended Mode

The Toolbar-Button »Extended Mode« allows to use the calculator beyond the original game rules in a more general way, e.g. with a variable number of operands. The slider »Number of threads to use for computation« allows to use a variable number of CPU cores.

Hint: To find an existing solution in the table, the easiest way usually is to use the »Sort last … first« button to sort the table »backwards« from the last to the first column. Start searching the last operation in the according column, then the second to last, and so on.

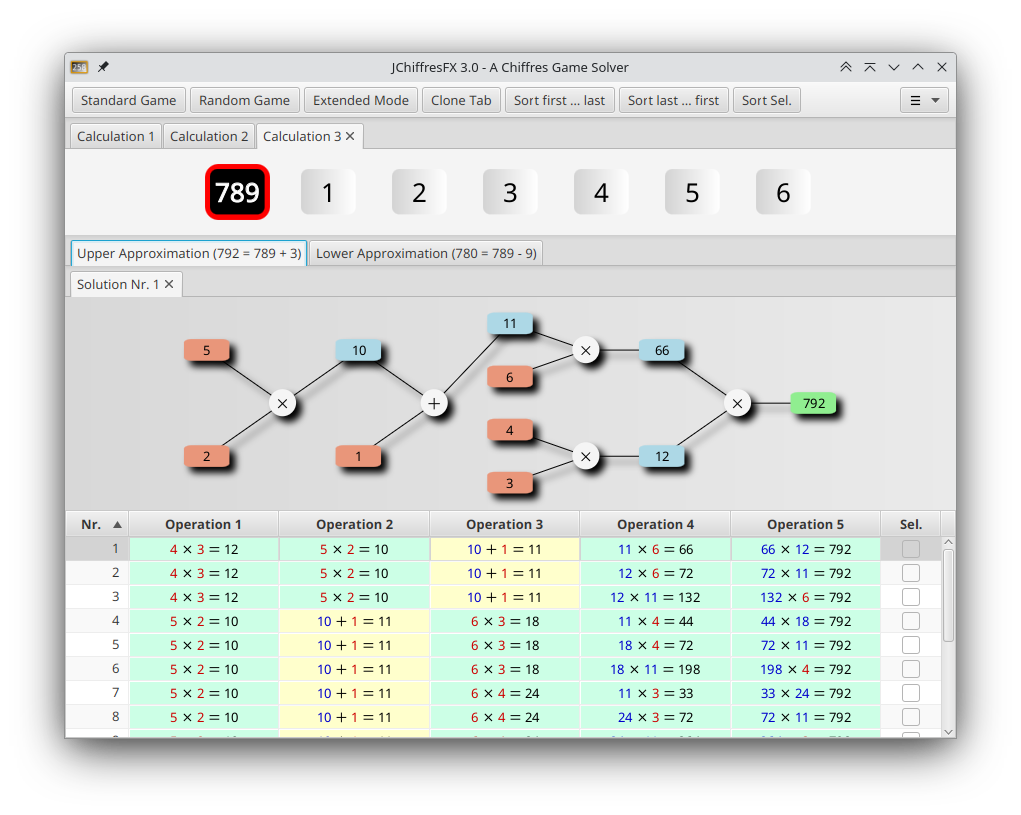
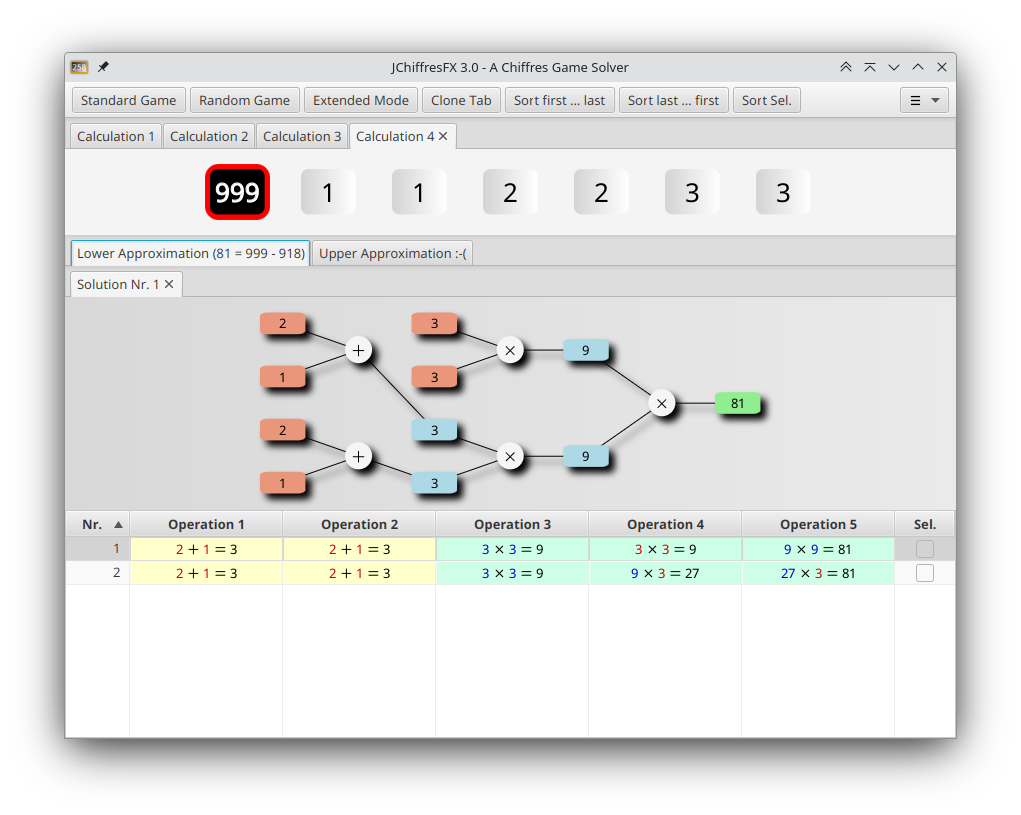
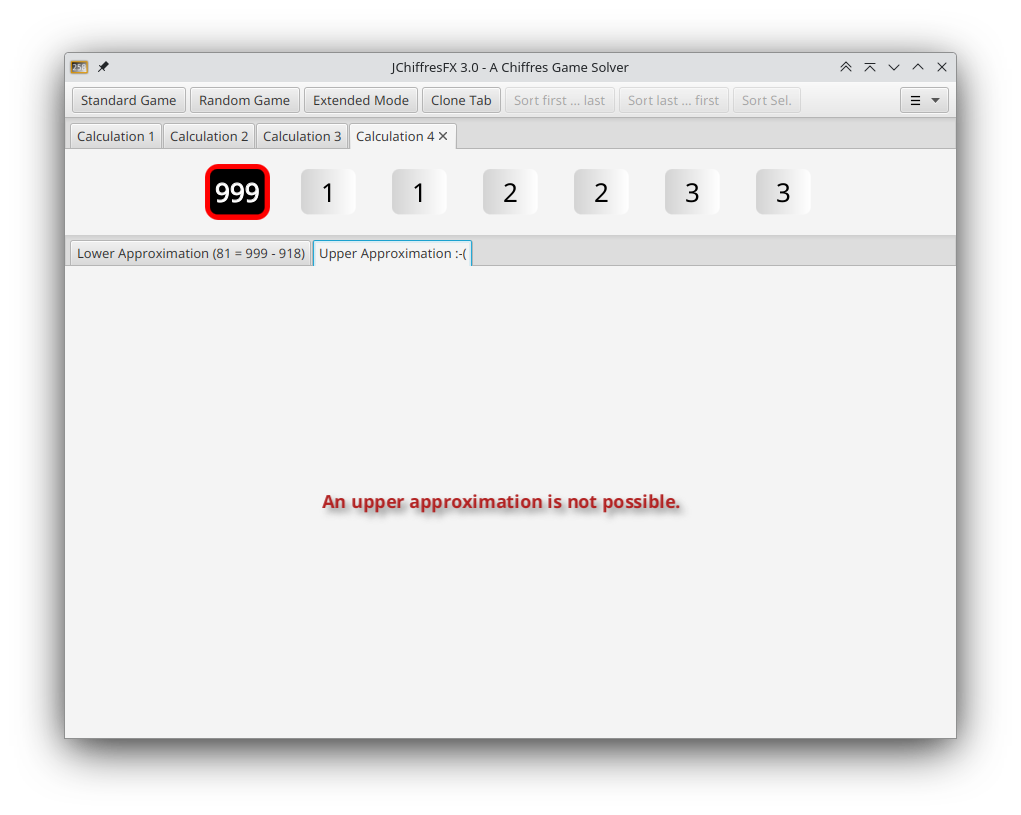
It is possible that no exact solution exists (e.g.: 1, 2, 3, 4, 5, 6 with goal 999). In this case the calculator searches for the best possible upper and lower narrowing solutions.

The Button »Clone Tab« opens a new tab initialized with the same operands as the current tab. This allows to intentionally search for a narrowing solution, even if there is an exact solution.